הקדמה:
בפוסט הזה, המבוסס על סיפור אמיתי (בקרוב הסרט…), נציג איך שיטות שונות יכולות לעזור לפתור בעיות מסוג מסוים.
וכמובן, שבתור אנליסטים – אי אפשר בלי לסבך קצת יותר ממה שצריך…
לכן – נציג 3 גישות שונות לפתרון בעיה 'עסקית', ועל הדרך נמחיש מהו ההבדל בין כלכלן לאנליסט ובין אנליסט לסטטיסטיקאי.
ולמה זה מעניין?
כי דאטה אנליסט טיפוסי נדרש להתמודד עם בעיות מאוד מגוונות, המחייבות היכרות עם צורות חשיבה שונות, וארגז כלים מגוון מאוד.
אה, ובגלל שהפוסט יכול לחסוך לכם את הקנס על Over Weight בפעם הבאה שתטוסו בחברת לואו קוסט…
סיפור המעשה
אז כמו כולנו, מדי פעם גם אני טס לחו"ל.
ועם הטרנד של טיסות הלואו קוסט – זה גם קורה הרבה יותר מבעבר…
באחת מהנסיעות האחרונות שלי החלטתי לקחת רק תיק גב, מאחר ולא ציפיתי שארכוש דברים (אגב, מזוודה/טרולי אפשר לקחת רק בתוספת תשלום).
 במהלך הטיול ההנחה הזו קצת השתנתה, לאחר שנתקלתי במחירים מצחיקים על בגדי חורף.
במהלך הטיול ההנחה הזו קצת השתנתה, לאחר שנתקלתי במחירים מצחיקים על בגדי חורף.
לכן, לקראת הטיסה חזור 'נתקעתי' עם יותר מדי קניות, ונאלצתי לקנות תיק בשביל לשלוח לבטן המטוס.
אחת הבעיות הגדולות היתה מגבלת המשקל של התיק – 10 ק"ג, שמעליה נדרש לשלם קנס על Over Weight (כ-50 אירו).
בגלל שלא היתה לי דרך למדוד את המשקל המדויק, וחששתי מהקנס, הערכתי אותו בצורה מחמירה למדי.
בשדה התעופה, גיליתי עד כמה מחמירה היתה ההערכה – התיק שקל קצת יותר מ-6 ק"ג בלבד.
מבאס…
בשביל שכזה דבר לא יחזור על עצמו, החלטתי להזמין באינטרנט משקל מזוודות נייד מיד אחרי הנחיתה בארץ, והוא הגיע לאחר זמן יחסית קצר.
אך כאשר קיבלתי אותו – גיליתי לתומי שאין הוראות ברורות איך להפעיל אותו.
מה עושים? כמובן – מתחילים לשקול איתו משהו.
התחלתי עם איזה תיק שהיה לי, ומיד הבנתי את גודל הטעות.
מסתבר, שהיה צריך לכייל את המשקל על 20 ק"ג בדיוק.
התיק שלי שקל כנראה בין 5-10 ק"ג, ככה שהמשקל החדש הראה נתונים שאין שום קשר בינם ובין המציאות.
ולא שינה כמה ניסיתי לכייל את המשקל מחדש – זה פשוט לא עבד…
בשלב הזה רוב האנשים היו מתייאשים וקונים משקל נורמלי.
רוב האנשים…
ועכשיו נשאלת השאלה (ותחשבו שיש לכם את השאלה הזו בראיון עבודה…):
מה אתם הייתם עושים בשביל להחזיר לחיים את 'המשקל הסורר'?
(קחו לכם כמה דקות לחשוב על זה. והנה רמז לכיוון של התשובה: שם המאמר הוא " מה ההבדל בין כלכלן לאנליסט "… )
הדרך הטריוויאלית לשקול תיק עם 'משקל סורר' (שיטת הכלכלנים)
כולנו מכירים את "המשקל".
לא זה של המזוודות, אלא ההוא שבודק אם אכלנו יותר מדי בשבוע האחרון…
לי אישית אין כזה בבית, אבל להורים שלי יש משקל אנלוגי כזה – ישן ונאמן, כזה שחווה הרבה עליות ומורדות (תרתי משמע…)
אז ניצלתי את אחד מסופי השבוע שבהם אני מבקר את ההורים – להיעזר בו בשביל להבין האם משקל המזוודות הסורר יודע לעבוד כמו שצריך.
התכנון היה לקחת חפץ מסוים, לשקול אותו עם המשקל התקין, אז עם המשקל הסורר ולקבל את היחס ביניהם.
במקרה הזה – אם עבור משקל של 10 ק"ג נקבל משקל מדוד של 23 ק"ג, נוכל להסיק שהיחס הוא 2.3 .
כך, בעתיד פשוט נמדוד ונחלק את התוצאה ב-2.3 לקבלת המשקל האמיתי.
האם זו התשובה שנתתם? כנראה שכן…
וכאן אתם יכולים לטעות, כי התשובה הזו קצת פשטנית מדי.
אגב, חשוב מאוד להדגיש, שקיימים המון מצבים, שבהם הגישה הפשטנית היא הטובה והמהירה ביותר.
אבל במקרה הזה – הגישה הזו עשויה להתברר כלא מספיקה.
מדוע?
כי יכול להיות אמנם שמדובר רק בתקלה של כיול.
אבל מצד שני, יכול להיות שיש בכלל תקלה במשקל הנייד עצמו.
ומאחר והמשמעויות הן הרות גורל (קנס של 50 אירו על Over-Weight, מה שיכול להרוס טיול שלם) לא מספיק פשוט לחשב את היחס בין המשקל האמיתי והמשקל הנמדד.
לכן – כדאי להעמיק מעט יותר בשביל להגדיל קצת את האמון במשקל הסורר.
וזו אחלה הזדמנות להמחיש מה ההבדל בין כלכלן לאנליסט , ולסטטיסטיקאי.
הדרך האנליטית 'לתקן' את ה'משקל סורר'
 אז איך אפשר לבדוק אם מדובר בתקלת כיול, או תקלת מדידה?
אז איך אפשר לבדוק אם מדובר בתקלת כיול, או תקלת מדידה?
הדרך המתבקשת היא איסוף וניתוח נתונים – הרבה תצפיות של משקל אמיתי ומשקל נמדד. כמות התצפיות והנתונים היא ההבדל המרכזי בין כלכלן לאנליסט (Data Analyst).
אם היחס יהיה יחסית קבוע – סימן שמדובר בתקלת כיול.
ואם היחס לא יהיה עקבי – כנראה שהמשקל פשוט צריך למצוא את דרכו לפח (סליחה – למחזורית).
איך עושים את זה?
לוקחים דלי, וממלאים אותו במים.
שוקלים אותו במשקל האמיתי ואז במשקל 'הסורר'.
לאחר מכן מתחילים לרוקן את הדלי במעט, מודדים שוב – וחוזר חלילה.
מומלץ כמובן לשקול מספר פעמים במשקל הסורר עבור כל כמות נתונה של מים בדלי.
כך, נקבל מספר תצפיות של משקל אמיתי ומשקל מדוד
(כלל אצבע שכדאי להכיר: רצוי מעל ל-30 תצפיות – בגלל 'משפט הגבול המרכזי' בסטטיסטיקה).
לבסוף, ניקח את כל התצפיות לאקסל ונחשב את היחס.
ומה אמורים לראות בשלב הזה?
עכשיו, ניכנס קצת לעולם הסטטיסטיקה, ודרכו נמחיש את ההבדל בין אנליסט לסטטיסטיקאי.
ולמי שפחות מכיר את העולם הזה – לא צריך להיבהל, כי אפשר לעשות ניתוחים מעט פשוטים יותר.
אם מדובר בבעיה של כיול, היחס המדוד (משקל סורר לחלק למשקל אמיתי) אמור להתפלג נורמלית.
מדוע?
כי אנחנו מניחים שמדובר בשגיאת מדידה, שיכולה להיות חיובית או שלילית.
ועכשיו אפשר לקחת את הניתוח לשני כיוונים מעניינים:
1. הגישה האנליטית
לעשות רגרסיה לינארית בין המשקל האמיתי למשקל המדוד – ולוודא שיש רמת התאמה גבוהה (השיפוע של הקו הלינארי אמור לצאת בדיוק היחס).
ואגב, למי שזה נשמע לו סינית – אפשר פשוט לשים את הנתונים על תרשים פיזור באקסל, ולהוסיף קו מגמה לינארי.
וכן, כמובן שרגרסיה לינראית היא שיטה סטטיסטית, אבל המימוש שלה באקסל עם קו המגמה הוא מאוד פשוט – ובמקרים רבים הוא גם אמור להספיק בשביל להגיע למסקנה יחסית מבוססת.
2. הגישה הסטטיסטית
לחשב רווח בר-סמך (הערכת היחס הממוצע האמיתי מתוך מדגם של ערכים – ברמת בטחון מסוימת – לרוב 95%/99%).
ולמי שזה נשמע סינית (או קוריאנית – אתם תחליטו) – כאן כבר קצת יותר קשה לעשות קיצורי דרך – צריך ללמוד סטטיסטיקה…
הגישה האנליטית
נתחיל עם האפשרות הראשונה – של קו מגמה לינארי, כי זו הדרך שמשקפת הכי טוב את דרך החשיבה של דאטה אנליסט;
ככלל, אם התוצאות של ניתוח אנליטי ראשוני באקסל יחסית ברורות – אפשר בהחלט להסתפק בהן (לא תמיד חייבים הוכחות סטטיסטיות).
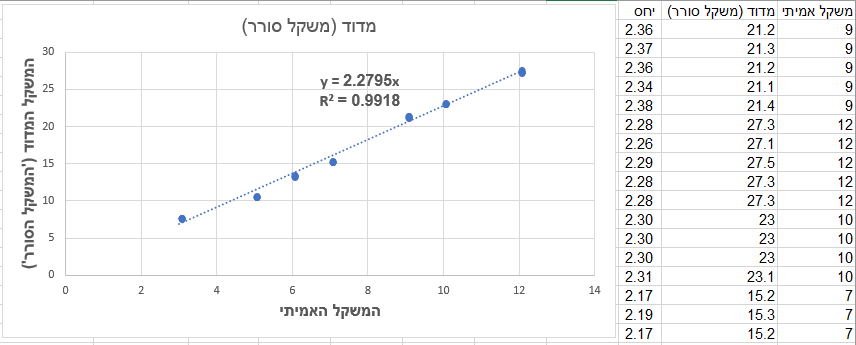
אז נשים את כל התצפיות על תרשים פיזור: משקל מדוד (של המשקל הנייד הסורר) מול המשקל האמיתי.
אם המשקל הסורר עובד בצורה תקינה, ורק מכויל לא נכון, אם נוסיף לתרשים הפיזור קו מגמה, אנחנו אמורים לקבל בדיוק קו לינארי.
השיפוע של קו המגמה אמור לתת בדיוק את היחס בין המשקל האמיתי למשקל הסורר.
אבל האם זה באמת מספיק?
התשובה היא שלא, מאחר וייתכנו 'רעשים במדידה' – הלא דלי עם מים על משקל אנלוגי זה לא הדבר הכי מדויק בעולם.
לכן – חשוב להסתכל גם על מדד טיב ההתאמה (R בריבוע) של קו המגמה (רגרסיה לינארית).
התוצאות לפניכם (נניח שניקח רק את הממוצע בכל משקל אמיתי):
טיב ההתאמה של המדידות הוא מעל ל-99% – מעיד על התאמה לינארית כמעט מושלמת.
לכן – כבר בשלב הזה אפשר להסיק שככל הנראה המשקל הנייד תקין – רק צריך לחלק את מה שהוא מראה ב-2.28!
הגישה הסטטיסטית לטיפול 'במשקל הסורר'
מבלי להיכנס יותר מדי לסטטיסטיקה (בכל זאת – זה פוסט, לא קורס…), נסביר מהו רווח בר סמך.
רווח בר סמך הוא נוסחה, המייצגת טווח שבו נמצא ממוצע אמיתי של אוכלוסייה או ערך מסוים, כאשר כל מה שיש לנו זה מדגם של אותה האוכלוסייה.
במקרה הזה, יש לנו מדגם של 30 תצפיות המתאר את היחס בין המשקל האמיתי למשקל הסורר, ואנחנו רוצים לחשב טווח שבו נמצא ממוצע היחס האמיתי.
עכשיו: כמובן שבכל תצפית יש טעות מדידה/דגימה. היא יכולה להיות קטנה מאוד או ענקית.
הרעיון של רווח בר סמך הוא לתת טווח שבו נמצא חלק גדול מאותה הטעות הסטטיסטית (נניח 95% או 99%).
את הנוסחה של רווח בר סמך איני רוצה לפרט כאן, מאחר וההסבר שלה קצת מורכב…
לכן, רק אציין שהיא תלויה ב-4 פרמטרים:
1. ממוצע יחס המשקל במדגם.
2. השונות (הפיזור של היחס סביב הממוצע).
3. מספר התצפיות במדגם.
4. רמת הביטחון שעבורו רוצים לקבל את הטווח (רמת בטחון של 100% תחזיר יחס של בין מינוס אינסוף לפלוס אינסוף…)
לאחר שנפעיל את הנוסחה, נקבל שיחס המשקלים הוא בטווח [2.22-2.35] ברמת ביטחון של 99%.
כלומר – שאם בעתיד נרצה לשלוח תיק לבטן המטוס, ו'המשקל הסורר' יציג עבורו את הערך 22 ק"ג,
נהיה בטוחים ב-99% שהמשקל האמיתי הוא פחות מ-10 ק"ג (החלוקה של 22 ק"ג בערך הגבול התחתון – 2.22 תיתן כ-9.9 ק"ג כהערכת המשקל האמיתי).
בפועל – כמובן שנעדיף לקחת מרכב בטחון מעט יותר גדול, אבל זה העיקרון.
סיכום
אז דרך הסיפור המעניין שלנו הבנו מה ההבדל בין כלכלן לאנליסט, ובין שניהם לסטטיסטיקאי:
1. גישה כלכלית (הנוטה להיות איכותית ולעיתים פשטנית)
2. גישה אנליטית (איסוף נתונים וניתוח מגמות עם תרשים)
3. גישה סטטיסטית (חישוב מדדים סטטיסטיים ברמת בטחון מסוימת)
דאטה אנליסט טוב אמור להכיר את כל 3 הגישות הללו, ולבחור בגישה המתאימה ביותר לראייתו למשימה הספציפית שמולה הוא מתמודד.
וכמובן – אם פועלים לפי מספר גישות – אפשר לחזק מאוד את המסקנות.
ואחרי שהבנו את כל זה – כל מה שנותר הוא לחפש עוד טיסה לחו"ל…

יפה מאוד!אהבתי!